Hay lugares geométricos, unidimensionales, que constituyen curvas no contenidas en un plano, sino que se mueven en las tres direcciones del espacio. Veamos algunos de ellos.
HÉLICES: Son curvas cuya tangente en cada punto mantiene un ángulo constante con respecto a un plano horizontal. Entre las hélices más singulares tenemos:
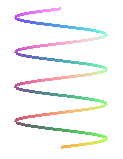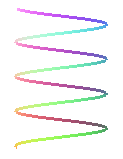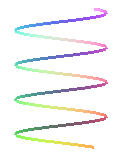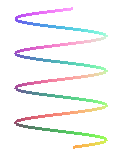
HÉLICE CILÍNDRICA: La curva se mueve sobre la superficie de un cilindro. Sus ecuaciones paramétricas vienen dadas por: 
, donde a y b son los semiejes de la sección elíptica y c mide el paso, es decir, la separación entre dos vueltas consecutivas de la curva.
HÉLICE CÓNICA: La curva se mueve sobre la superficie de un cono. Sus ecuaciones paramétricas vienen dadas por: 
, donde a y b son los semiejes de la sección elíptica y c mide el paso, es decir, la separación entre dos vueltas consecutivas de la curva.
HÉLICE ESFÉRICA: La curva se mueve sobre la superficie de una esfera. Sus ecuaciones paramétricas vienen dadas por:
HELICOIDE
Es la superficie mínima de la hélice. En el caso del helicoide cilíndrico podemos escribir sus ecuaciones paramétricas: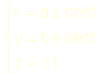
El Helicoide, edificio de Caracas.
