LUGARES GEOMÉTRICOS EN EL ESPACIO: Es un conjunto de puntos del espacio que verifican una misma propiedad.
En un curso habitual de geometría del espacio en bachillerato se estudian diversos lugares geométricos sencillos. Por ejemplo, el PLANO MEDIADOR de un segmento es el conjunto de puntos del espacio que están a igual distancia de un segmento dado. O lo que es equivalente, el plano perpendicular al segmento por su punto medio. De la misma manera, un PLANO BISECTOR es el conjunto de puntos del espacio que está a igual distancia de dos planos que se cortan. Es decir, divide en dos partes iguales el ángulo diedro formado por los dos planos secantes, por lo que, en realidad, habría dos planos bisectores.
ESFERA: Es el lugar geométrico de los puntos del espacio que están a igual distancia de un punto dado (centro). Si el centro tiene coordenadas (a, b, c) y el radio es r, la ecuación cartesiana de la esfera se obtiene expresando algebraicamente la condición dada: (x - a)² + (y - b)² + (z - c)² = r².
Las ecuaciones paramétricas vienen dadas por  .
.

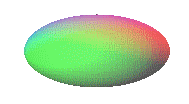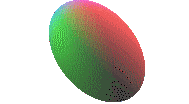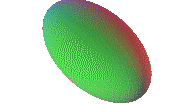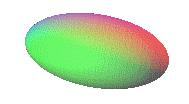
La esfera es un caso particular del ELIPSOIDE, cuyas ecuaciones paramétricas son muy similares:
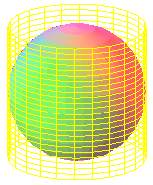
ARQUÍMEDES Y LA ESFERA
Arquímedes de Siracusa (h. 287 a. C. - h. 212 a. C.) estudió la relación existente entre los volúmenes y las áreas de la esfera y el cilindro. Puedes comprobar que son iguales las áreas del cilindro y la esfera inscrita en él: 4pr².
Sus métodos de cálculo pueden considerarse precursores del actual cálculo integral.
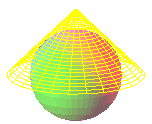
SUPERFICIES CÓNICAS: Fijado un punto del espacio P(a, b, c) y una curva C(f(t), g(t), h(t)), el conjunto de todos los puntos pertenecientes a todas las rectas que unen P con cada punto de C constituye una superficie cónica de vértice P y directriz C.
Por tanto, las
ecuaciones paramétricas de tal superficie serán:  .
.

Podemos obtener un sencillo caso particular con una circunferencia como curva directriz, tomando las ecuaciones C(cost, sent, 0).
Pero C no tiene por qué ser siempre una curva cerrada.

CARTOGRAFÍA
Tanto el cilindro como el cono son figuras desarrollables en un plano; por tanto, ambas pueden servir para proyectar la esfera y poder trazar mapas planos de la esfera terrestre.
SUPERFICIES CILÍNDRICAS: Fijado un vector v(a, b, c) y una curva C(f(t), g(t), h(t)),
el conjunto de todos los puntos pertenecientes a todas las rectas que cortan a C con dirección v constituye una superficie cilíndrica de directriz C y generatrices paralelas a v.
Las ecuaciones paramétricas de tal superficie son:  .
.

Al igual que en el caso de las superficies cónicas, el caso más conocido es aquel en el que la curva directriz es una circunferencia.
Pero hemos de advertir que, también, las superficies cilíndricas pueden tener curvas directrices abiertas...

MECÁNICA
Muchas veces hablamos sin pararnos a pensar en lo que decimos: motor de ocho cilindros en V...

SUPERFICIES DE REVOLUCIÓN: Una curva C(f(t), g(t), h(t)) que gira en torno a un eje E (recta) genera una superficie de revolución. En el caso en que E es el eje OZ, las ecuaciones paramétricas de la superficie vienen dadas por:  .
.

Algunas de las superficies que ya hemos visto, son también superficies de revolución.
Así, un cono cuya curva directriz es una circunferencia, es una superficie de revolución generada por una recta que gira en torno a otra.
La esfera es una superficie de revolución generada por una circunferencia que gira en torno a uno de sus diámetros. Etc.
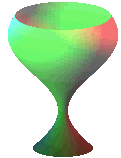
TORNO
Tanto el torno de mecánico como el de alfarero o el de ebanista, nos permiten generar superficies de revolución.

SUPERFICIES DE TRASLACIÓN: Dadas las curvas C(f(t), g(t), h(t)) y D(m(t), n(t), p(t)) que se cortan en el punto P(a, b, c) se genera una superficie de traslación al desplazarse paralelamente a D cada uno de los puntos de C, de forma que P va recorriendo todos los puntos de D. Las coordenadas paramétricas de dicha superficie son:  .
.

Un cilindro de sección circular también puede considerarse una superficie de traslación.


LA TÉCNICA
La técnica requiere el uso de las superficies de revolución por sus específicas características geométricas.

CUÁDRICAS: Son superficies cuya ecuación implícita es un polinomio de segundo grado en x, y, z. De alguna manera están asociadas a las cónicas. Exponemos los casos particulares en que los ejes de las cuádricas coinciden con los ejes de coordenadas:

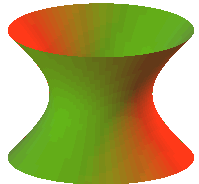

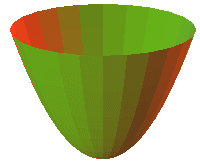
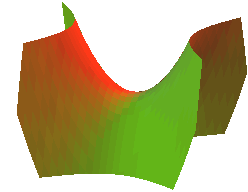
LA ARQUITECTURA
No hay más que prestar un poco de atención a nuestro alrededor, o mirar el mundo a través de revistas o de la televisión, y podremos darnos cuenta de la profusa utilización de este tipo de superficies en edificios, muchas veces emblemáticos.


