OTROS LUGARES GEOMÉTRICOS EN EL PLANO: A lo largo de la historia se ha intentado dar respuesta a numerosos retos planteados, unas veces para resolver algún problema de tipo técnico, otras veces para satisfacer la curiosidad del ser humano, sin que esto quiera decir que luego no haya encontrado aplicación práctica en otro momento, como ya se vió en el caso de las cónicas.
En ese proceso de investigación se estudiaron muchas curvas realmente sorprendentes.
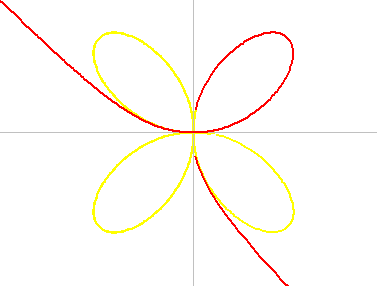
CICLOIDE: Es la curva que describe un punto fijo C de una circunferencia cuando ésta rueda sobre una recta. Si tomamos un punto H en el mismo radio que C pero interior al círculo, la curva que describe H se denomina HIPOCICLOIDE. En cambio, si tomamos un punto E exterior al círculo, sobre la prolongación del mismo radio, se obtiene una EPICILOIDE
Ecuaciones paramétricas de la cicloide: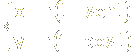 
, donde r es el radio de la circunferencia.
LA CICLOIDE COMO TAUTÓCRONA
Esta curva fue bautizada por Galileo en 1590. Ha ocupado el interes de los más grandes sabios del siglo XVII.
Huygens (1673) descubrió la propiedad TAUTÓCRONA de la cicloide: el período de un péndulo 'guiado' por la cicloide no depende de su posición inicial ni de su longitud: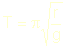 
. Este resultado era de vital importancia para controlar la precisión de los relojes de péndulo que habían de viajar a bordo de barcos.
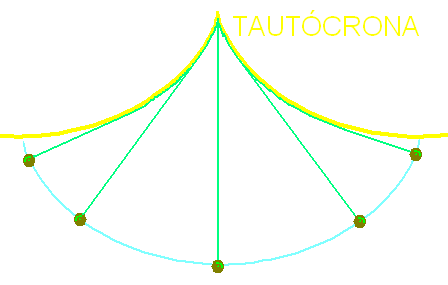
Además, la trayectoria seguida por el péndulo es también una cicloide
HIPOCICLOIDES: Son curvas descritas por un punto fijo P de una circunferencia que rueda por el interior de otra circunferencia. Su forma depende de la razón entre el radio de la circunferencia fija R y el de la circunferencia móvil (generatriz) r. En el caso en que R/r = 4 la curva recibe el nombre de ASTROIDE.
Ecuaciones paramétricas de la hipocicloide: 
.
Ecuaciones paramétricas de la epicicloide: 
.
EPICICLOS
Los astrónomos de la Antigua Grecia utilizaron los epiciclos para explicar el movimiento de retroceso aparente de algunos astros, afirmando que éstos seguian una trayectoria epicíclica alrededor de cierto círculo llamado deferente.
El pintor alemán Alberto Durero (1471 - 1528) utilizó ampliamente los métodos geométricos en el arte, e inició en 1525 un estudio sistemático de hipocicloides y epicicloides, aunque estos estudios pasaron desapercibidos entre los matemáticos.
Desargues (1593 - 1662), matemático francés, aplicó el estudio de las epicicloides a la construcción de engranajes de rozamiento mínimo.
En 1687, Newton, en sus Principia, generaliza los estudios de Huygens sobre el péndulo cicloidal estableciendo que en un campo de atracción esférico, las líneas de oscilaciones isócronas del péndulo representan una epicicloide.
ESTROFOIDE: Dadas dos rectas, que pueden ser los ejes de coordenadas, fijamos un punto A en una de ellas (por ejemplo semeieje negativo de abscisas) y un punto P en la otra (semieje positivo de ordenadas). A cada lado de P determinamos dos puntos E1 y E2 que están a igual distancia de P que el origen de coordenadas. El lugar geométrico de estos puntos E1 y E2 cuando P se desplaza por el eje de ordenadas es la estrofoide.
La ecuación cartesiana de la estrofoide es: 
, donde a es la distancia entre A y el origen de coordenadas.
PTEROIDE
Probablemente fue el científico francés Roberval (1602 - 1675) el primero que estudió esta curva, en 1645, y le dio el nombre de pteroide (pteron = ala).
El nombre estrofoide es debido a Montucci (1846) y viene del griego strofos que significa 'cordón, cuerda, lazo, correa'.
"
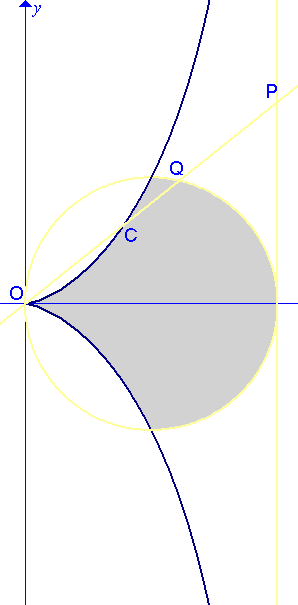
CISOIDE DE DIOCLES: La ecuación cartesiana de la cisoide viene dada por: 
, donde a es el radio de la circunferencia. En coordenadas polares tenemos: 
, y en paramétricas: 
NACIDA PARA DUPLICAR
Diocles (ca. 240 - ca. 180 a. C.) fue un matemático griego que ideó esta curva con el objetivo de resolver el problema de la duplicación del cubo.
La cisoide se define como el lugar geométrico de los puntos C que verifican que |OC| = |QP|.
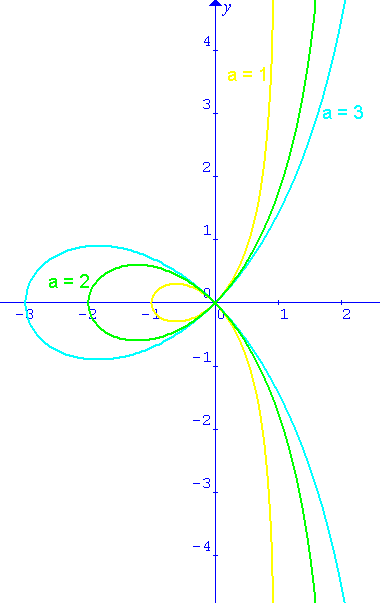
FOLIO DE DESCARTES: Su ecuación cartesiana se escribe habitualmente x³ + y³ = 3axy.
En coordenadas polares viene dada por: 
.
Podemos observar cierta
similitud con la cisoide si comparamos sus coordenadas paramétricas, 
Esta curva fue utilizada en 1638 por Descartes para refutar el método de Fermat para hallar tangentes.
DE JAZMÍN A FOLIO
Durante mucho tiempo fue mal representada: una vez hallado el bucle, supusieron que se repetía simétrica y perpendicularmente por lo que se le dio el nombre de flor de jazmín.
No conviene precipitarse...
VERSIERA DE AGNESI: Dada una circunferencia de diámetro OA = a, cortamos éste por un punto B mediante una recta perpendicular al mismo que. a su vez corta a la circunferencia en un punto C. Sobre dicha recta se toma un punto M que cumple: BM : BC = OA : OB. Cuando el punto C recorre la circunferencia, el punto M describe una curva que recibe el nombre de versiera de Agnesi. Traduciendo algebraicamente esta condición, se obtiene su ecuación: 
LA BRUJA
El nombre de versiera es debido al científico italiano Guido Grandi que la estudió y publicó en 1718 algunas de sus particularidades.
El motivo es que, como podemos observar en el gráfico, BC es al seno del arco OC, mientras que BA es lo que se conocía como sinus versus de dicho arco. Grandi quiso hacer referencia a este término, pero no cayó en que la palabra versiera, en italiano, también significa 'bruja'.
Teniendo en cuenta, además, que Agnesi [Maria Gaetana Agnesi] era mujer, no parece sonar muy bien eso de "la bruja de Agnesi".
Feminismo [¡fundamentado!] del s. XVIII:
“Si en algún momento puede excusarse la temeridad de una mujer, que se atreve a aspirar a las sublimidades de una ciencia que no conoce límites, ni siquiera los de la infinitud misma, ciertamente debería ser en este período, en el que reina una mujer, ... En esta época ... toda mujer debería esforzarse, y empeñarse en promover la gloria de su sexo”
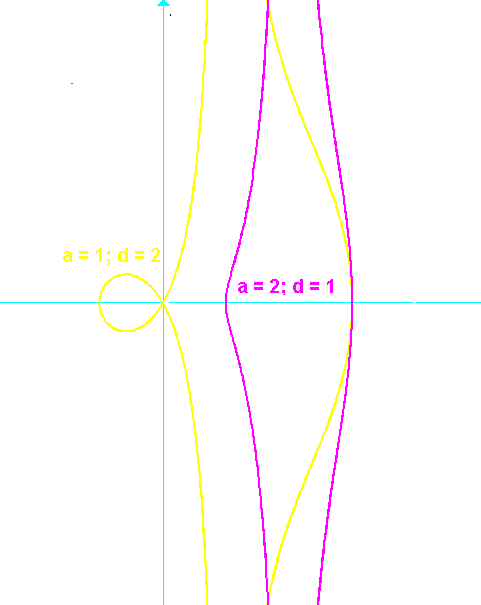
CONCOIDE DE NICOMEDES: Dado un punto O (polo) y una recta b (base) a una distancia a de dicho punto, trazamos una recta arbitraria r que pase por O y corte a b en el punto P. Sobre esta recta r, a ambos lados de P, y a una distancia d, se toman dos puntos C1 y C2. El lugar geométrico de estos dos puntos cuando P recorre b, describe una curva que recibe el nombre de concoide de Nicomedes.
Si tomamos el polo como origen de coordenadas y el eje de abscisas perpendicular a la base, la ecuación de la curva es: 
.
En coordenadas polares: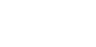 
, y en paramétricas: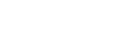 
EN FORMA DE CONCHA
Nicomedes fue un matemático de la Antigua Grecia contemporaneo de Eratóstenes (276 - 194 a. C) que construyó esta curva para aplicarla a la resolución de uno de los tres problemas clásicos de la geometría: la trisección de un ángulo que, como es sabido, no es resoluble utilizando sOlo regla y compás (salvo en casos muy concretos). Para construir la curva inventó un dispositivo llamado concoidógrafo.
El nombre concoide significa en forma de concha (de molusco).
