CARDIOIDE: Se construye de manera análoga a la concoide, pero sustituyendo la recta base b por una circunferencia. Así, partimos de un punto O (polo) sobre una circunferencia de diámetro a, y un segmento de longitud d. Trazamos por O una recta arbitraria que corta a la circunferencia en un punto P. Sobre esta recta, a ambos lados de P y a una distancia d, se obtienen los puntos M1 y M2 que generearán la curva cuando P recorre la circunferencia.
La ecuación cartesiana de la cardioide es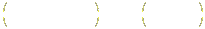 
. En coordenadas polares: 
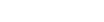. Y en paramétricas: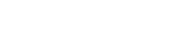 
EL CARACOL DE PASCAL
Esta curva también se conoce con el nombre de caracol de Pascal, en honor de Etienne Pascal (1588 - 1651) padre del famoso científico francés Blaise Pascal (1623 - 1662). El nombre fue propuesto por Roberval, quien consideraba que era una de las formas de la concoide generalizada.
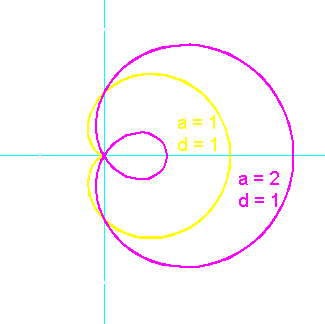
Según los valores que vayan tomando a y d, se obtienen diversas formas de la curva. (Puede comprobarse en el applet desplazando el centro de la circunferencia y/o el punto A, que no tiene por qué estar sobre ella).
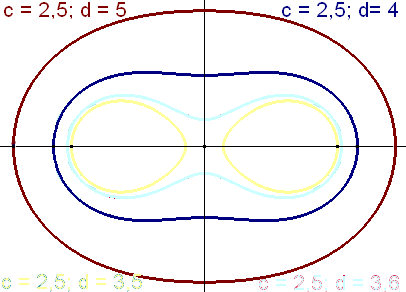
CURVAS DE CASSINI: Dado un segmento FF' de longitud 2c y y una distancia d, se llama curva de Cassini al lugar geométrico de los puntos M del plano tal que el producto de las distancias a los extremos del segmento F y F' (focos) es igual al cuadrado de la distancia d.
La ecuación cartesiana de la curva resulta, pues, 
. Y tomando el punto medio O de FF' como polo y el semieje OX positivo como eje polar, obtenemos su ecuación en forma polar 
.
CASSINIS
El famoso astrónomo italiano Giovanni Domenico Cassini (1625 - 1712) suponía que esta curva podría representar más exactamente la órbita de la Tierra que una elipse. Esto fue hecho público en 1749 por su hijo, también astrónomo, Jacques Cassini. Aunque esa hipótesis no pudo confirmarse, la curva fue objeto de numerosas investigaciones.
A veces se la nombra como óvalo de Cassini, aunque, como podemos ver, hay veces que no tiene forma ovalada.
LEMNISCATA DE BERNOUILLI: Caso particular de curva de Cassini, en que d = c.
Podemos escribir las ecuaciones paramétricas: 
.
LEMNISCUS
Esta curva surgió en 1694 en un trabajo sobre las mareas de Jacques Bernouilli (1654 - 1705)
Curiosamente no se estableció la identidad entre la lemniscata y el ocho de Cassini hasta 1806, por el matemático italiano Saladini.
La palabra lemniscata proviene del latín 'lemniscus' que significa lemnisco: cinta de adorno en la corona de los vencedores o de los invitados a un banquete.
Alcanzó amplia fama cuando en 1718, el matemático italiano J. C. Fagnano (1682 - 1755) descubrió interesantes propiedades al intentar calcular la longitud de un arco de la curva: la integral correspondiente no se puede expresar mediante funciones elementales, pero la curva se puede dividir en n arcos iguales con regla y compás para determinados valores de n.
TRACTRIZ: El arquitecto francés Claude Perrault propuso en 1693 a los matemáticos el siguiente problema: Un punto material P (de un plano) está fijado al extremo de un hilo no elástico. El otro extremo del hilo tenso se desplaza sobre una recta r (del mismo plano). ¿Qué línea describe el punto P? El problema fue resuelto, simultaneamente, por Leibniz y Huygens, que llamó a la línea buscada tractriz.
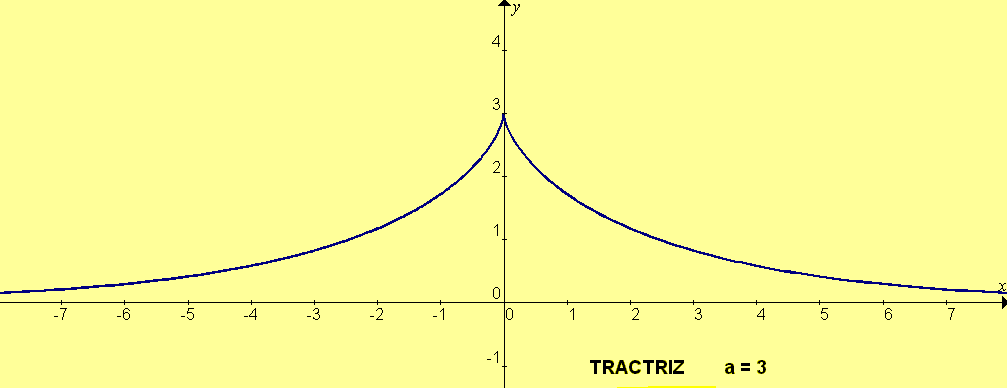
Las ecuaciones paramétricas de la tractriz pueden escribirse: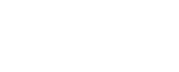 
, donde a es la "altura" de la tractriz:
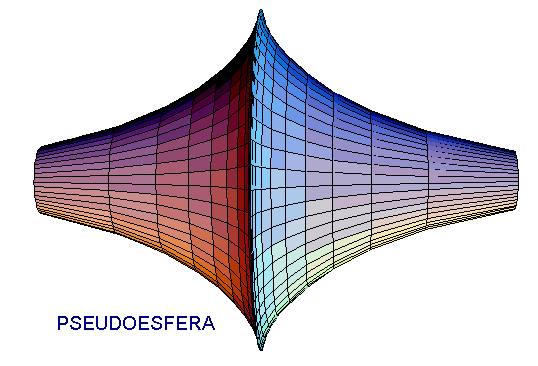
PSEUDOESFERA
Si hacemos girar la curva en torno a su asíntota (el eje de abscisas en el caso de la imagen) se obtiene un cuerpo de revolución llamado PSEUDOESFERA. Aunque en la imagen no podemos mostrarlo, este cuerpo no tiene principio ni fin. Sin embargo, su superficie tiene un valor finito: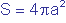 
. Y su volumen también: 
.
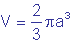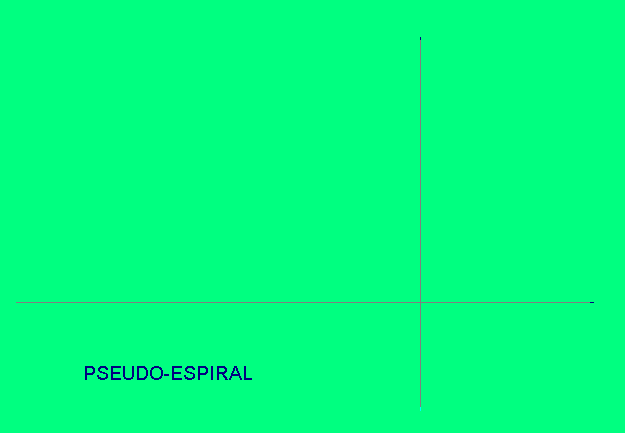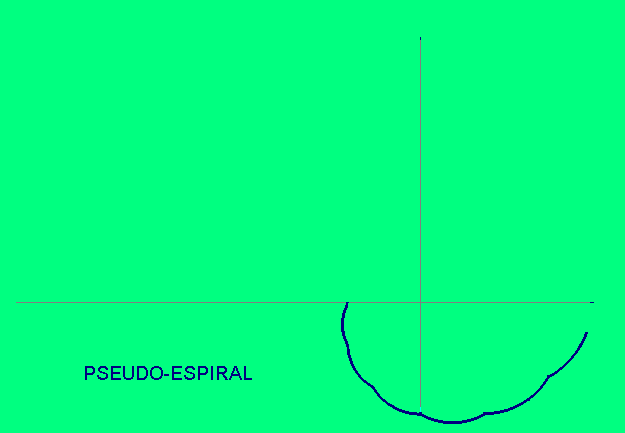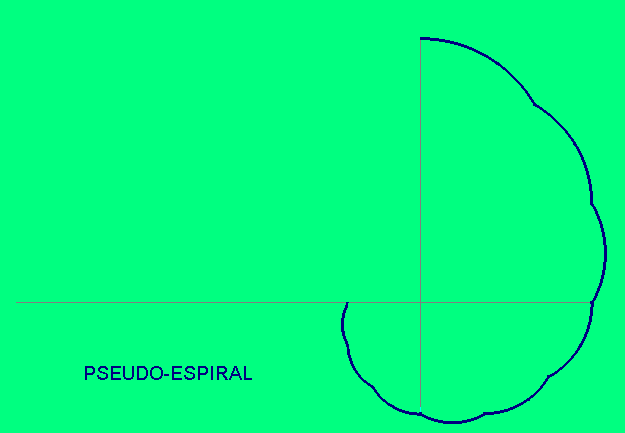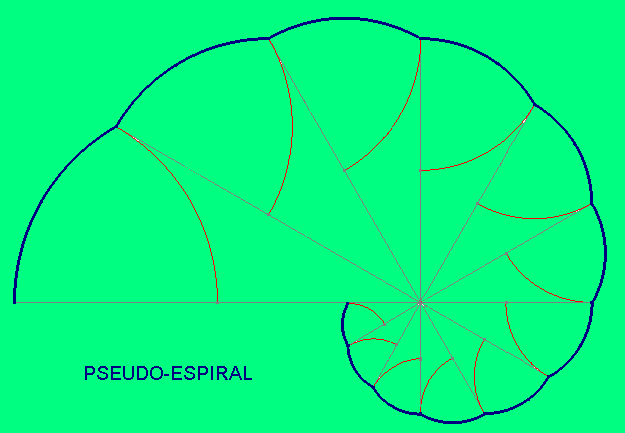
ESPIRALES. Son curvas generadas por un punto que gira en torno a otro (centro) al mismo tiempo que se aleja de él. Hay diversos tipos de espirales según sea la relación entre el ángulo de giro y la distancia al centro.
